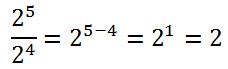why the sum of two sides of triangle is greater than the third side and their difference less than the third side

in the triangle ABC
AB + BC > AC
because the straight line is the shortest distance between two points
and by taking away BC from both sides then
AB + BC - BC > AC - BC
AB > AC - BC

imagine math: multiplying mixed numbers

imagine math: multiplying mixed numbers: "when multiplying mixed numbers we first convert them to improper fractions before multiplying , for example"

prime number

a prime number has exactly two positive divisors itself and one .
1)now  is the number zero is a prime number ?
no because the zero divisible by any nonzero number so it has an infinite numbers of divisors
2) is the number one is a prime number ?
no because the number one has one positive divisor is itself
3) is the number two a prime number ?
yes because the number two divisible by one and it self so it has two divisors one and it self and the number two is the only even prime number
so we can define the prime number as it greater than one and has no divisors other than one and itself

multiplying mixed numbers

when multiplying mixed numbers we first convert them to improper fractions before multiplying , for example

mixed number arithmetic

we can add or subtract two mixed numbers in one of two ways
1) first strategy is to add the whole numbers and then to add fractions , for example

2) second strategy is to convert the mixed numbers into improper fractions before adding them , for example

to convert an improper fraction into a mixed number

first we will review the parts of division problem  and the rule is

in an improper fraction the numerator is the dividend and the denominator is the divisor . but in the mixed number the quotient is the whole number and the remainder is the new numerator and the denominator is the divisor
to convert an improper fraction to a mixed number divide the numerator into the denominator and the remainder will be a new numerator and the quotient will be a whole number , for example

mixed numbers and improper fractions

1) what is the improper fraction ?
is a fractions whose numerator is larger than its denominator for example

2) what is the mixed number ?
a mixed number consist of the sum of whole number and a fraction. for example

now we will writing the mixed number as an improper fraction
1)to convert a mixed number  into an improper fraction, we multiply the
whole number by the fraction’s denominator and then add this to the numerator.
The sum is the new numerator.

the rule is
 
2) by another method

compound fractions

what is the fraction ?
the fraction is dividing the numerator by the denominator for example

but a compound fraction is a fraction where the numerator or denominator or both are fractions , for example

now we want to find the product of 
 


we say three contain 6 halves so that

then the rule of the compound fractions is

Albert Einstein

Albert Einstein was born in the German city of Ulm on March 14, 1879 and spent age Ivaath in Munich.His father was a "Hermann Einstein" works in the sale of feathers used in the manufacture of pillows, and his mother worked "Ni Pauline hut" with him in the management of a small workshop to manufacture electrical appliances after giving up the profession of selling feathers. Delayed Einstein child in pronunciation even three years old, but he showed a passion for great nature, and the ability to understand mathematical concepts difficult, has been studied alone Euclidean geometry, and in spite of his membership in the Jewish, the income of Einstein's middle school a Catholic and received lessons in playing the violin, but Einstein rejected the idea of ​​personal god and religions are full and his private letters show that he believed in Spinoza's God is nature. In five years old his father gave him a compass, and Einstein realized then that there is strength in space are influencing the compass needle and you move. He was suffering from difficulty in comprehension, and was probably due to the shyness in childhood. Rumour has it that Einstein's child had failed the math later, however, likely that the amendment in the evaluation of grades students then raised that the child had been delayed and Einstein failed in mathematics. And the adoption of two of uncles Einstein's care and attention that child support science in general Vzodah books related to science and mathematics. After repeated losses of the workshop set up by his parents in 1894, his family moved to the city of Pavia in Italy, took advantage of Einstein's son the opportunity to withdraw from school in Munich, which dislike the strict regime stifling, and spirit. And he spent Einstein years old with his parents in the city of Milan in order to show that he must determine the way in life shuddered to his high school in the town of Arua, Switzerland, and progress after the exams the Swiss Federal Institute of Technology in Zurich in 1895, was like Einstein's methods of teaching it, and was often Maigtta of his time to study physics alone, or playing the violin, that passed the examinations and graduated in 1900, but the teachers did not choose him to enter the university.

why any number to the zero power except zero gives 1

you know that when dividing numbers with the same base , raised to the powers , we subtract the power of the divisor from that of the dividend .

now

and we know that any number divisible by zero has no meaning
finally
any number to the zero power except zero gives  1

The Least Common Denominator

our goals to add or subtract two fractions having the same denominator . now we could compute

and

while 18 is a common denominator in the above example and 6 is the smallest common denominator

adding and subtracting fractions with unlike denominators

if we need to find the sum or difference of two fractions having different denominators , then we must rewrite one or both fractions so that they have the same denominator
for example
now we find the sum

it is difficult to add
then we use equality of two fractions

now we add three twelfths and four twelfths and the product equal seven twelfths

finally

adding and subtracting fractions with like denominators

if we want to add or subtract two fractions having the same denominators we only need to add or subtract their numerators . the rule is

and

for example 
now we examine the sum of one third and two thirds . we adding one third to two thirds give us a total of three thirds which agree with  the formula

the Greatest Common Divisor

The Greatest Common Divisor
Fortunately there is a less tedious method for writing a fraction in its lowest
terms. We find the largest number that divides both the numerator and the
denominator. This number is called the greatest common divisor (GCD). We
factor the GCD from the numerator and denominator and then we rewrite
the fraction in the form:

simplifying fractions

When working with fractions, we are usually asked to “reduce the fraction to
lowest terms” or to “write the fraction in lowest terms” or to “simplify the fraction.”
These phrases mean that the numerator and denominator have no common
factors (other than 1). For example, 2/3 is in written in lowest terms but 4/6 is not
because 2 is a factor of both 4 and 6. Simplifying fractions is like fraction multiplication
in reverse. For now, we will use the most basic approach to simplifying
fractions. In the next section, we will learn a quicker method.
First write the numerator and denominator as a product of prime numbers.
(Refer to the Appendix if you need to review finding the prime factorization of
a number.) Next collect the prime numbers common to both the numerator and
denominator (if any) at beginning of each fraction. Split each fraction into two
fractions, the first with the common prime numbers. This puts the fraction in
the form of “1” times another fraction. This might seem like unnecessary work
(actually, it is), but it will drive home the point that the factors that are common
in the numerator and denominator form the number 1. Thinking of simplifying
fractions in this way can help you avoid common fraction errors later in algebra.

multiplying fractions and whole numbers

now if we want to multiply 4 X 2/9 we can imagine a circle and we divided it to 9 equal parts if we have 2 parts and we repeated it to 4 times then we have 8 parts of 9 parts
              then               4 X 2/9 = 8/9

fraction multiplication

the rule for multiplying fractions  a/b X c/d = ac/bd for example we using this rule to compute 2/3 X 1/4 . by multiplying the numerators 2 and 1 and the denominators 3 and 4 we obtain 2/12
now by another solution if we imagine two thirds of a quarter
we divided a quarter into 3 equal parts then whole one contain 12 equal parts then two thirds of a quarter = 2/12

equality of two sets

two sets S and T are equal if each element of S is an element of T and vice versa this is denoted S = T .
and inequality is

sets

sets is a collection of objects & a set is denoted by listing elements between braces

for example { 1 , 4  ,  8 }
and we do not count multiplicities we regard the set { 1 , 2 , 2 , 2 , 3 , 3 } as identical to the set { 1 , 2 , 3 } and order is not significant in sets and the set { 1 , 2 , 3 } is equivalent to the set { 3 , 2 , 1 }
and in enumerating the elements of the sets we use ellipse to indicate patterns . we denote the positive integers as { 1 , 2 , 3 , ......... } . we also denote the sets with the notation { x : condition on x } for sets that are more easily described than enumerated and this is read as " the set of elements  x such that x ....." .
and the Cartesian product of two sets is the set of the ordered pairs

and the Cartesian product of n sets is  the set of ordered n-tuples

why the product of two negative integers is positive

because the multiplication operation is a repeated addition operation
for example
(-3) x (-2) = - ( 3 x -2 ) = - ( (-2) + (-2) + (-2) ) = - (- 6 ) = 6  and 6 is positive integer

why the product of two positive integers is positive

because the multiplication operation is a repeated addition operation
for example
2 x 3 = 2 + 2 + 2 = 6   and  6 is positive integer